cscx等于什么（cscx等于什么三角函数）

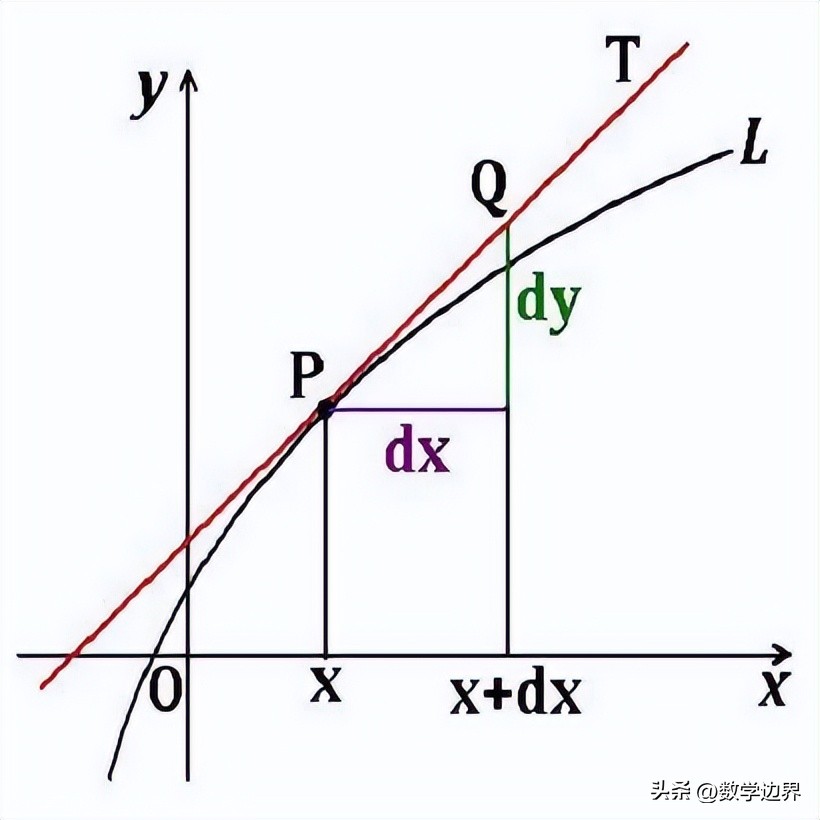
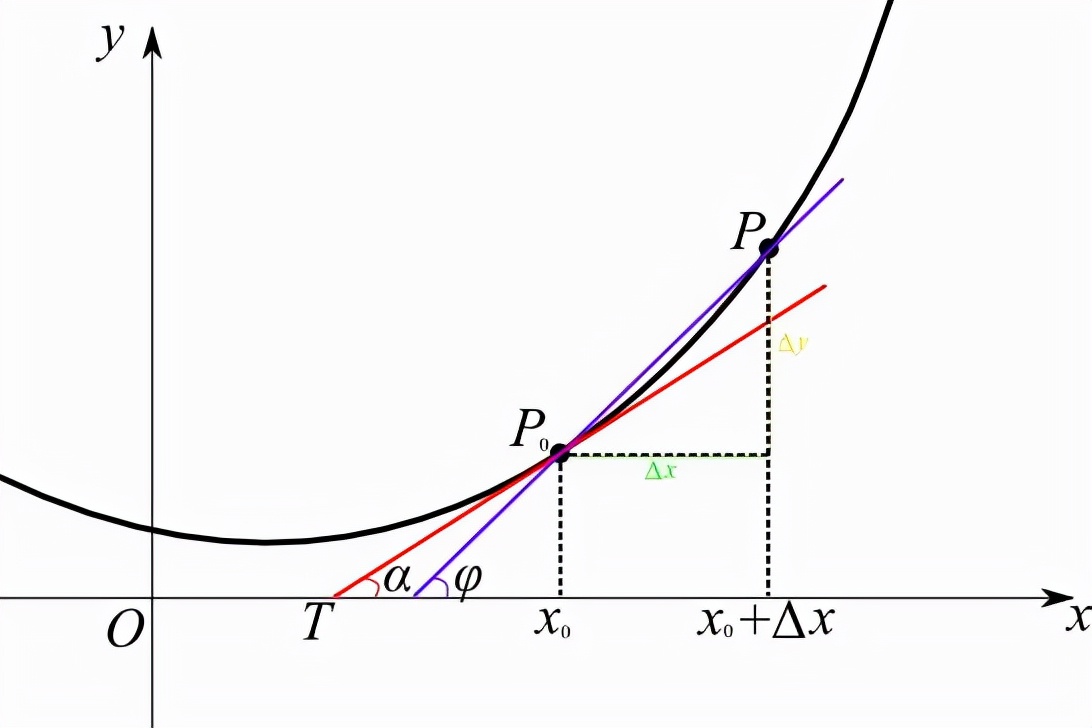
那我们怎么来求出这个切线的斜率呢？我们首先在函数图像上取两点

=lim[cosxsin(△x)/△x]

(x)′=1，(x^2)′=2x，(1/x)′=-1/(x^2)

(√x)′=[x^(1/2)]′=(1/2)×x^(1/2-1)

[log(a,x)]′=1/(xlna)

C为任意常数

(cotx)′=-(cscx)^2

这里y0=f(x0)，y0+△y=f(x0+△x)

指对数函数的导数就讨论到这里，接下来我们来讨论三角函数的导数。

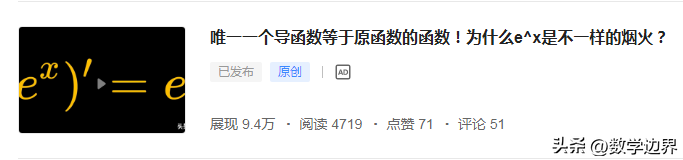
(e^x)′=e^x

(x^n)′=nx^(n-1)，n∈N*

我们首先来求幂函数的导数

(e^x)′=e^x，[ln(x)]′=1/x

根据两角和差公式

y=arcsinx，x=siny

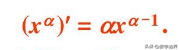
y(x)=a^x

=lim[sinxcos(△x)+cosxsin(△x)-sinx]/△x，△x→0

我们都学习过导数，对于普通数学爱好者而言，可以说导数就是区分初等数学和高等数学的分界岭。今天我们就来聊聊到底什么是导数，基本初等函数都是如何求导的？

=lim{[f(x0+△x)-f(x0)]/△x}

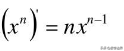
=cosxlim[sin(△x)/△x]，△x→0

(√x)′=1/(2√x)，(C)′=0

文章链接：

根据换底公式

利用复合函数求导法则

dy=d(x^n)=[nx^(n-1)]dx

(C)′=(Cx^0)′=C(x^0)′

(arcsinx)′=1/√(1-x^2)

(x^2)′=2×x^(2-1)=2×x^1=2x

=[x^(-1/2)]/2=1/(2√x)

y′=dy/dx=d(x^n)/dx=nx^(n-1)

ln[y(x)]=ln(a^x)=xlna

=cosx×1=cosx，△x→0

(tanx)′=(secx)^2

x^α=[e^(lnx)]^α=e^(αlnx)

(1/x)′=[x^(-1)]′=(-1)×x^(-1-1)

y′=y′(x)=f′(x)=lim(△y/△x)

[log(a,x)]′=(lnx/lna)′=(lnx)′/lna

注意到arcsinx∈[-1,1]?(-π/2,π/2)

接下来我们来讨论指对数函数的导数，我在前面的文章中已经详细讨论了利用自然常数e的定义，可以证明(e^x)′=e^x。

y′(x)=dy/dx=1/(dx/dy)

利用这个结论，我们就可以求出以e为底的自然对数函数y=lnx的导数

1=x×y′(x)

=nx^(n-1)△x+C(n,2)x^(n-2)(△x)^2+…+(△x)^n

(arccosx)′=-1/√(1-x^2)

lim(sinx/x)=1，x→0

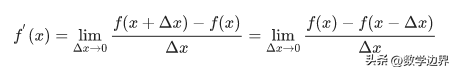
(x+△x)^n-x^n

y=log(a,x)，a＞0且a≠1

=lim{[nx^(n-1)△x+C(n,2)x^(n-2)(△x)^2+…+(△x)^n]/△x}

(x)′=(x^1)′=1×x^(1-1)=x^0=1

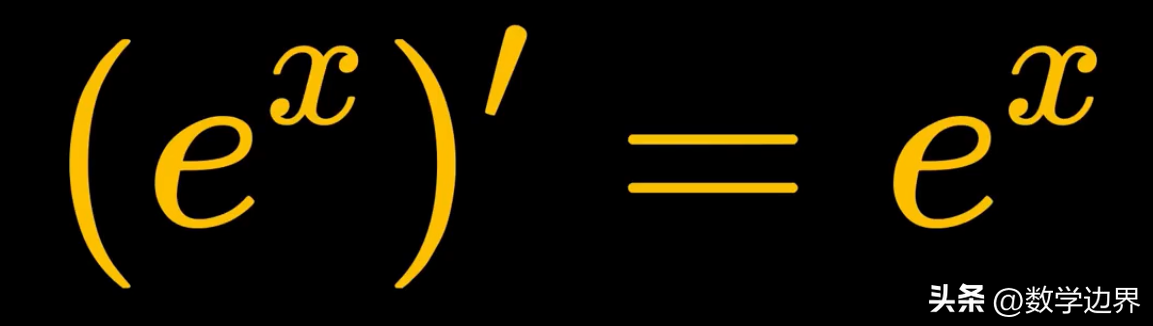
好了，关于基本初等函数的导数就介绍到这里。在整个推导过程中，运用到了多种不同的求导方法，值得大家认真体会。

(sinx)′=cosxlim[sin(△x)/△x]

由于证明过程比较复杂，有兴趣的朋友可以前往我的主页翻看一下。

=x^α×α×(lnx)′

[1/y(x)]×y′(x)=lna×(x)′=lna×1=lna

=nx^(n-1)+0+…+0=nx^(n-1)

我们还可以将以上结论中的正整数n拓展到任意实数α。

(x^α)′=[e^(αlnx)]′=e^(αlnx)×(αlnx)′

根据拓展到实数域的结论，我们可以很快得出几个常见导数。

函数y=f(x)在定义域内每一个点的导数所构成的函数称为函数的导函数，记为y′=f′(x)。

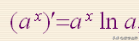
lim[sin(△x)/△x]=1，△x→0

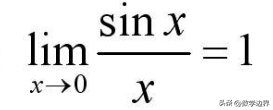
k=y′(x0)=f′(x0)

(x)′=[e^y(x)]′=[e^y(x)]×y′(x)

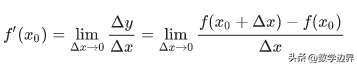
=√[1-(siny)^2]=√(1-x^2)

=(1/x)/lna=1/(xlna)

[(y0+△y)-y0]/[(x0+△y)-x0]

{ln[y(x)]}′=(xlna)′

http://www.toutiao.com/origin/article/7197230973258678822/

(sinx)′，△x→0

利用后面将要证明的

根据二项式定理：

=[x^n+nx^(n-1)△x+C(n,2)x^(n-2)(△x)^2+…+(△x)^n]-x^n

连接直线P0P，这里P0P就是函数图像的一条割线。当△x→0的时，x0+△x→x0，点P也就逐渐趋近于点P0，割线P0P趋近于过点P0的切线，割线P0P的斜率也就趋近于这条切线的斜率。这个过程的极限值就是函数在点x0的导数。

类似地，我们还可以求得

=lim(△y/△x)，△x→0

(a^x)′=(a^x)lna

=lim[sinx+cosxsin(△x)-sinx]/△x

cosy=cos(arcsinx)＞0

y′(x)=[ln(x)]′=1/x

首先来求正弦函数y=sinx的导数

割线P0P的斜率等于

(arctanx)′=1/(1+x^2)

=C[0×x^(0-1)]=C×0=0

=lim[nx^(n-1)+C(n,2)x^(n-2)(△x)+…+(△x)^(n-1)]，△x→0

(arccotx)′=-1/(1+x^2)

dx/dy=d(siny)/dy=(siny)′=cosy

我们把自变量x的增量△x用dx表示，称为自变量的微分；把因变量y的增量△y用dy表示，称为因变量的微分。那么导函数又可以表示为：

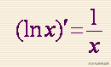
导数定义、微分定义、二项式定理、复合函数求导法则、对数恒等式、反函数定义、自然常数e的定义、换底公式、两角和差公式、正弦重要极限、反三角函数定义等。

y(x)=ln(x)，x=e^y(x)

y′(x)=y(x)lna=(a^x)lna

(cosx)′=-sinx

x=e^(lnx)

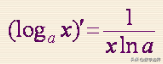
△y=f(x0+△x)-y0=f(x0+△x)-f(x0)

过点P0的切线的斜率

(x^n)′=lim{[(x+△x)^n-x^n]/△x}

(x^α)′=αx^(α-1)，α∈R

(x^n)′=lim{[(x+△x)^n-x^n]/△x}

总结一下，本文运用到的方法和知识点有：

r=0，1，2，…，n

dx/dy=cosy=√(cosy)^2

类似地，我们还可以求得

=△y/△x

=αx^α×(1/x)=αx^(α-1)

y′=y′(x)=f′(x)=dy/dx，dy=f′(x)dx

(sinx)′=cosx

同样对于一般对数函数求导

=lim{[f(x+△x)-f(x)]/△x}，△x→0

=-x^(-2)=-1/(x^2)

根据重要极限

=lim[sin(x+△x)-sinx]/△x

最后我们来对反三角函数求导，我们以反正弦函数为例：

函数y=f(x)在点x=x0的导数就是指函数图像在点x0处的切线的斜率k，记作k=y′(x0)=f′(x0)。

(a+b)^n=Σ[C(n,r)×a^(n-r)×b^r]

对于n∈N*，△x→0

也可以写成：y=x^n

进一步对于任何底数a＞0且a≠1的指数函数y=a^x求导

根据对数恒等式

=1/√(1-x^2)

P0(x0,y0)和P(x0+△x,y0+△y)